A previous study on bovine tuberculosis (TB) in the northern lower peninsula of Michigan used multivariate conditional logistic regression in a case-control design (Kaneene et al. 2002). Kaneene et al. (2002) used 18 covariates and deer TB prevalence summarized in 3 x 3 blocks (~23 km2) in an area surrounding farms that resulted in P-values and Odds Ratios of risk of disease. Note that this design does not borrow from strength or knowledge of data from adjacent areas.
An alternative way is to link the disease status (positive or negative) of each farm sampled to some landscape-level predictors. This is a multi-step process that can be done in WinBUGS with data prepared in R or ArcMap depending on your level of experience or comfort with either program. There are 3 major considerations to approaching spatial epidemiology that was used in a study on bovine tuberculosis on cattle farms prepared in ArcMap that is the basis for this section (Walter et al. 2014):
1. Spatial Resolution
First we overlayed a 5 x 5 km grid having a resolution of 25 km2, which is approximately equal to a quarter township in size. We selected quarter townships as the proper resolution given that township would likely be too coarse a scale and section would be too fine a resolution for model convergence based on previous research with Bayesian hierarchical models (Farnsworth et al. 2006, Walter et al. 2011). This would result in a total of 368 cells covering the Modified Accredited Zone (MAZ; 5 counties) in Michigan and we can then assign the value associated with each landscape-level predictor variable to a farm in our study based on the grid cell that an individual farm was sampled from; thus, all farms sampled from within a particular grid cell were assigned the same value for each landscape-level predictor.
2. Covariates
It is very important that covariates are based on some a priori knowledge of factors contributing to an increase in risk for infection of disease. To simply data dredge and hope some covariates are contained within the top model(s) is wrong and a study should not be designed this way. Researchers designing a study on spatial epidemiology should consider the demographic variables of the host and/or reservoir and well as any environmental or landscape variables that may influence host/reservoir distribution in the landscape. To simply include elevation, slope, and aspect because previous researchers included them is simply incorrect and should be avoided.
3. Distribution of data
The spatial extent of the data across the study area of interest is also of importance due to limitations in computer processors. If the spatial resolution is small and the extent is large and results in >2000 cells across your study region, it may take weeks to run models or models may not run at all. The spatial extent of the data that would be suitable to achieve objectives of the study should be determined prior to initiating studies using Bayesian hierarchical modeling in WinBUGS.
9.6.1 Adjacency matrices with weights = 1
Spatial resolution can be handled and incorporated into modeling efforts using Intrinsic Gaussian Conditional Autoregressive Models (ICAR) in WinBUGS using:
car.normal(adj[], weights[], num[], tau)
where:
Adjacency - a vector listing the ID numbers of the adjacent areas for each area (this can be generated using the Adjacency Tool in R or ArcMap)
Number - A vector of length N (the total number of areas) giving the number of neighbors for each area
Weights - A vector the same length as adj[] giving unnormalized weights associated with each pair of areas
Thus, the random effect of the jth grid cell is conditional on the values of its (usually = 8) neighboring cells. Adjacency matrices were created with the Adjacency for WinBUGS Tool that provides a matrix relating one areal unit to a collection of neighboring areal units in text files for use in WinBUGS (Fig. 7.1). In ArcMap, an adjacency matrix can be created by installing a Toolbox created by the USGS that will result in 3 separate textfiles. Results of these textfiles can be used within your program to run models in WinBUGS.
1. Install Adjacency for WinBUGS Tool and follow program page for setup.
2. Create the adjacency matrix in the GUI that will result in 4 text files although we will only need to use first 2 in our models:
(a) Adj.txt identifies each cell by unique ID that is adjacent to cell 1, cell 2, cell 3, etc., in sequential order (NOTE: Cell ID is not in file, only IDs of adjacent cells)
2,3,4,40,
1,3,4,5,8,39,40,44,
1,2,4,5,8,
1,2,3,
2,3,6,7,8,39,43,44,
5,7,8,9,12,43,44,48,
5,6,8,9,12,
(b) Num.txt identifies the number of neighbors for each cell in Adj.txt
4853885
(c) Raw.txt is similar to Adj.txt with the exception that the first number refers to the cell ID that the neighboring cells are adjacent to.
(d) SumNumNeigh.txt shows the overall numbers of neighbors that will be manually entered into WinBUGS code.
9.6.2 Adjacency weights other than 1
If we don't want the adjacent 8 cells having equal weight, we can have weights based on neighbours that share common boundaries (Rook) or that share common boundaries and vertices (Queen). There are also distance-based matrices that can incorporate proximity, population densities, or covariates such as age or sex (Earnest et al. 2007). Spatial resolution other than equal weight in the surrounding 8 cells can be handled and incorporated into modeling efforts using Conditional Autoregressive Models (CAR) in WinBUGS and can be created using the GeoDa program.
Earnest et al. (2007) identifies terms to describe several adjacency matrices that were based on neighborhood or distances that included:
1. Queen - neighborhood-based that refers to neighbors that share common boundaries and vertices (n=8 neighbors)
2. Rook - neighborhood-based that refers to neighbors that share common boundaries only (n=4 neighbors)
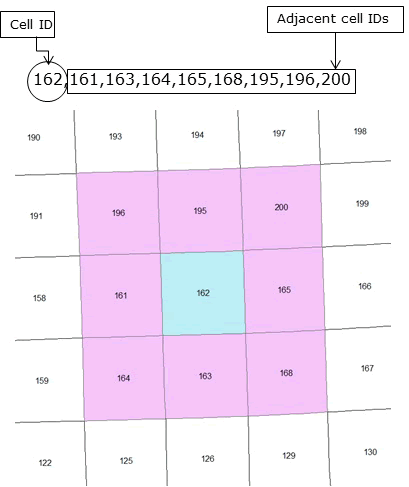
Figure 9.1: Adjacency matrix created in ArcMap using the Adjacency Toolbox.
3. Weights - distance-based that refers to neighbors at various distances away are less influential
4. Gravity - distance-based that refers to neighbors that are more populated have greater influence
5. Entropy - distance-based that refers to neighbors that are closer provide more weight than those farther away
6. Density - distance-based similar to Gravity except refers to neighbors that have greater density and not just population size so takes into account area
7. Covariate - distance-based that identifies a priori knowledge of a variable as influential in determining a regions or cells disease rate
9.6.3 Covariates
We can extract covariates within each grid cell for any variable we have a priori knowledge that it may influence potential for transmission of TB. For example, the Michigan Department of Agriculture and Rural Development (MDA) provided georeferenced data and herd size (i.e., number of cattle per farm) for all farms in the 5 county area of the Modified Accredited Zone (MAZ) that encompassed about 8,074 km2 of white-tailed deer habitat. We could have included a herd size effect in all models because these effects have been shown to influence Mycobacterium bovis (the bacteria responsible for TB) presence on farms or infection probability for farms in Europe (O'Reilly and Daborn 1995, Hutchings and Harris 1997, Phillips et al. 2003).
The main components of initiating a WinBUGS model section include:
1. Check Model
2. Load Data
3. Compiling chains
4. Load initial values

